Chapter 17 - The Sine and Cosine Function

I see crowds of People, walking around in a Ring. T.S. Eliot Wasteland

A current under sea Picked his bones in Whisper. As he rose and fell
He passed the stages of his age and youth
Entering the whirlpool. Wasteland

Your memory of trigonometry is probably filled with meaningless identities and strange acronyms to help remember what all the Trig. Functions refer to. Some of you may recall that infamous Indian Tribal Chief, SohCahToa, whose name helped you pass your equally notorious quizzes and tests. ( Sine opposite over hypotenuse, Cosine adjacent over hypotenuse, Tangent, opposite over adjacent; hence SohCahToa) Others may remember being presented with a circle, called the Unit Circle for reasons soon to be seen. In this circle any point on it had the co-ordinates ( Cos Ø, Sin Ø) where x= Cos Ø and y= Sin Ø. Often times the circle added more confusion to your understanding of Sines and Cosines. At such a point your mind must have justifiably asked, . What do Indian Tribal Chiefs and Circles have to do with the study of the Sine function, a function whose application arises everywhere from the ten second swaying period of a supertall skyscraper to the mechanisms that translate the back and forth motions of the watch spring into time. In almost any study of oscillating or vibrating systems, the Sine function arises, for reasons that are not attributed to mere coincidence and chance.

In all simplicity the Sine function is the complex mathematical function to describe circles. From the lines from T.S Eliot's Wasteland and from your own experience circles represent a never ending, repetitive cycle. Motion along a circle passes through the same point infinite times. It is this complex nature of the circle, that causes its study to be so intense and intricate. Before we can talk about circle, we need to first understand triangles.

Let us begin our study of the Sine function with a look at right triangles. In all simplicity the Sine of an angle ( The issue of what is an angle and how to describe it will be dealt with later) is the ratio of the opposite side to the hypotenuse:

Or more directly:

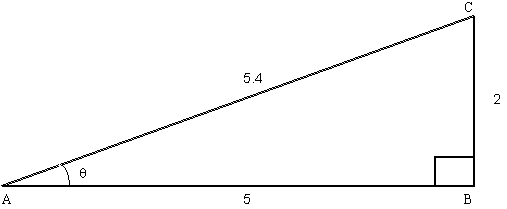
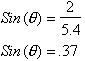
From the calculator or a Trig. Table we can find the angle q approximately. The Cosine functions similar to the Sine function except that it measures the  adjacent side, not the opposite side, ratio to the hypotenuse. For example:

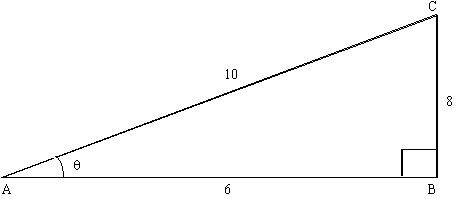
In right triangle ABC,

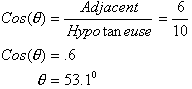
The last trig. Function, the Tangent, is the ratio of the opposite side to the adjacent side. Thus in right-triangle ABC,

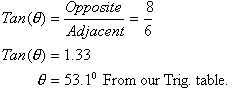
The remaining Trigonometric functions; Secant, Cosecant, and Cotangent are simply the reciprocal values of the Cosine, Sine, and Tangent respectively.

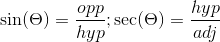
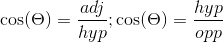
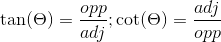
It is not important to remember the reciprocal functions as they unnecessarily add confusion to one.s understanding of Sine.s and Cosine.s and Tangent.s. It is enough to remember that they are just 1 over the value for the Sine, Cosine or Tangent.

To further make life easier one can express Tan (q) as just Sin (q) over Cos (q). This is easy to see as:

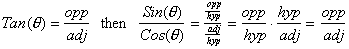
This reduces the study of Trigonometry to only two functions, the Sin (q) and Cos (q). Any other Trig function can be expressed as a variation of these two. To state them again they are:

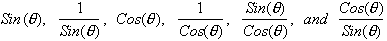
At this stage your mind should only be focused on knowing what  the Sine and Cosine of an angle mean. Sine is opposite over hypotenuse, and Cosine is adjacent over hypotenuse.

Now there are two very important concepts to understand about the Sine and Cosine of a given angle. First, Sines and Cosines apply only to right triangles, when there is one right angle of 90 degrees, whose opposite side is called the hypotenuse. If one were asked to find the Sine of the following angle.

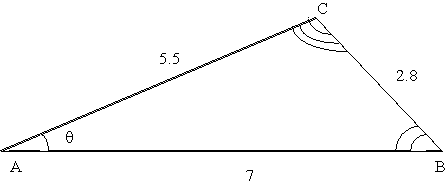
Then the answer is not 2.8/5.5 or 2.8/7 as triangle ABC is clearly not a right triangle and side AC is not a hypotenuse. To find Sin (q) we would have to somehow construct a right triangle, probably the easiest way by drawing an altitude from C perpendicular to AB, like this:

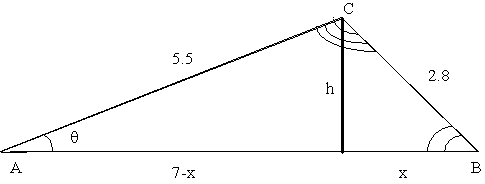
The values for h and x can be found by writing two simultaneous equations based on Pythagoreans's theorem:

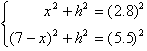
The second important point to understand about Sines and Cosines of angles is that their values are independent of the dimensions of the triangle. What this means is that the Sine of a 62 degree angle will always be .883, regardless of the size of triangle it is measured in.

Size is a meaningless quantity unless it is used with reference to something else. If you examine a right triangle individually then you will find it impossible to describe its size. It is only when you look at it with respect or relative to another triangle that you can correctly say the following concerning these two right triangle.

Triangle A is large. (Relative to B only)

Now if we were to compare Triangle A with let us say another Triangle C we would say:

Triangle A is small. ( relative to C)

Finally we can compare Triangle A with two other triangles and say the following:

Triangle A is of average size. ( relative to b and C).

This brings us to a logical question; how can Triangle A be small, large, and even average? Since Triangle A is unique and does not change then it is our adjectives which are at fault in describing the attribute of size of the triangle. We are now in a position to state an important philosophical idea: Adjectives are only as accurate as the number of objects an object is described relative to. In other words to describe something one must have at least a standard to compare it to.

As we mentioned before descriptions are only as accurate as the number of objects it is compared relative to. For this reason calling Triangle A average was more accurate than calling it large or small. This is because, in describing Triangle A as average we were comparing it relative to two triangles and not just one as in the other two cases.

The importance of understanding relativity cannot be understated in describing any situation, phenomena, object or attribute. To name but a few examples from the natural world, weight, velocity, size, distance and objects and light. Relativity can also be taken a step further to ask what in this world is absolute, or whose existence is independent of anything else. In the SI units of measurement, every quantity except length, time and mass are considered derived. For example volume, density , force etc.. can all be expressed in terms of the fundamental quantities of length, time and mass. But are length, mass and time, independent of each other?

Returning back to our discussion of the Sine function we saw that the Sine of an angle was simply the opposite side over the hypotenuse. We also now see how all other trigonometric functions can be expressed as variations of the Sine function alone,  with the help of the Pythagorean theorem. Therefore before continuing let us go through a simple proof of the Pythagorean theorem, a theorem which as you already know, arises almost everywhere in Mathematics.

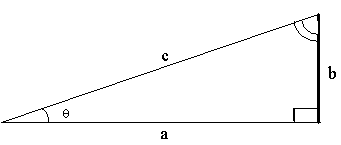
We begin this proof by drawing an altitude in a right triangle ABC,

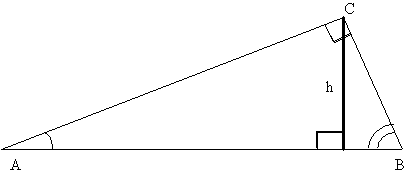
The altitude with height, h, divides the triangle into two other right triangles, both similar to triangle ABC.

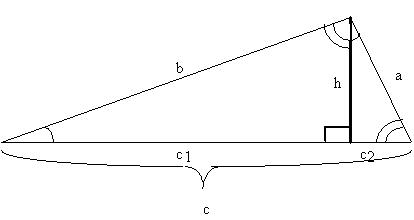
Viewing these three triangles together:

As these triangles are all similar we can state two identities:

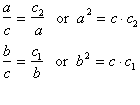
Adding a²  with b² gives us:

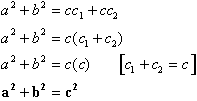
Taking the theorem a step further we can prove the following important identity relating sine with cosine. In any right triangle ABC

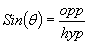
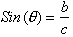Cos (q) would then be equal to a/c; however by the Pythagorean theorem; 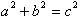, we can then re-write a as

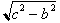
Hence:

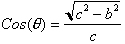
Squaring both sides gives us:

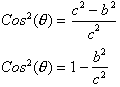
Remember that

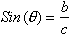
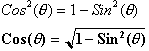
This identity holds true for any  right triangle. For remembrance sake it can also be written as; 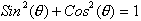This useful identity tells us that even the Cosine of an angle can be expressed in terms of the Sine of the angle, therefore the Sine function is the fundamental Trigonometric function, as all other functions can be derived from it, including the Cosine function.

Until now we have restricted our study to triangles, where the Sine of an angle is the ratio of the opposite side to the hypotenuse. We can therefore define the Sine function to be the function that outputs a unique ratio for an inputted angle. But we must ask ourselves what is an angle, and how can we express the sine of an angle mathematically without having to look up Trig. Tables? The solution is left for the next chapter that will go into detail to define the Sine function mathematically by using a circle and arclength.