Numbers and their uses
Chapter 2 - Understanding Numbers
Section 2.1 - Numbers and their Uses
What
is a number? What do all those abstract symbols floating about really mean? To
begin with, we can define the number as an existence. So if I had a few tennis
balls, the number of balls would simply refer to how many individual tennis
balls I am actually holding. 4 balls would mean four existences or :
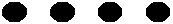
2 balls would mean
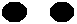
A number therefore does not depend on any specific quality of the object. 10
balls and 10 eggs are the same number of things.
Now
that we have defined the number as something created by the human mind to count
objects, then let us proceed to examine the Laws of Arithmetic.
The
laws of arithmetic are based on the addition and multiplication of numbers. But
what does it mean to add two or three numbers together? To begin with
addition assumes that all your numbers refer to something and that thing is the
same throughout. So 3 pens added with 3 pens is six pens. We are bringing together
all our things and then counting the sum. So:
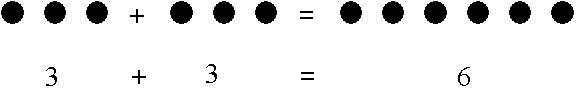
In
multiplication we are doing something a bit different, we are creating
multiples of a number. When we multiply two numbers x and y : we are creating y
multiples of x which is the same as adding x with itself y times. This can also
be thought of as a grid of x rows and y columns where the product of the
numbers is the sum of all the objects inside the grid. So 4 * 6 is:
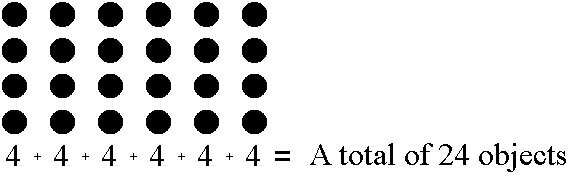
In this example we only added 4
with itself 6 times and summed up the number we got. This is all that
multiplication is about, creating multiples of a number or just repetitive
addition. Multiplication of two numbers x and y can therefore be expressed as:
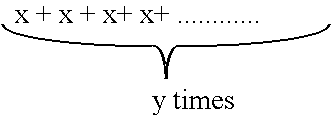
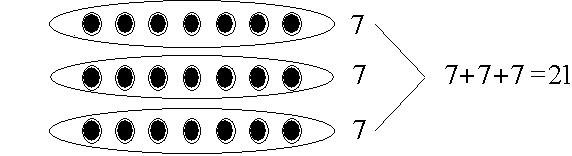
or 3*7 is: 7 + 7 + 7
You are probably asking what is the
use of such an operation or why is multiplying numbers an important
thing in mathematics. It is fairly obvious how it is used when
a baker wants to find the total cost of
42 cupcakes at $2/cupcake. The answer is 42*2. But is not so easy to understand
for example why in Newton's second Law of Motion:
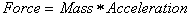
or why interest earned in money is:
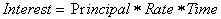
The reason multiplication dominates
these equations and so many others depends entirely on the context of the equation
and where it is derived from. As we study many equations in this book the
difference between multiplication and addition will become clearer.
We have studied integers which refer to full existences such as 2 books, 4
cats and 110 bananas. But what about half a candy bar or a third of a day?
When the existence or object is broken up into equal parts we say we are
dividing and we use fractions to represent the division. Division is
essentially the opposite or inverse operation of multiplication. Whereas
multiplication creates equal sets of a number, division creates equal
sub-sets within the number. The fractions that are used to represent division
are often written as:
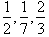where the bottom number refers to how many pieces the object has
been broken into. For example the following rod has been broken into 8
partitions where each small block is:
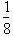’th of the original object:
We can now define x divided by y to be
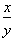where y indicates
the number of equal parts an object is subdivided into and x indicates how many
parts you have. The relationship between multiplication and division is best
expressed by the equation,
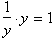If there is an x on top of the y it tells us that there
are x times
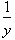or x parts of
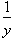
Whereas division creates sub-sets within an object,
multiplication creates sets outside the object. Dividing an object by another
number x, creates x sub-sets within the object such that multiplying one
sub-set by x give the original object
again. For this reason multiplication and division are called inverse operation
of each other.
We can now state the five laws of arithmetic:
1) A + B = B + A
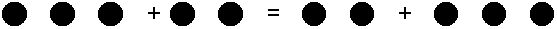
2) A + ( B + C)= ( A + B) + C
3) AB = BA
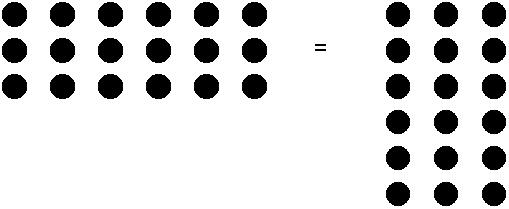
4) A(BC) = (AB)C
The fourth property is saying that
multiplication of more than two numbers is independent of the order they are
multiplied in.
5) A( B + C)= AB + AC
To this point our discussion of
numbers has been limited to positive numbers but what about negative numbers? Before
discussing what it means to have -3 books let us look at the number 0. Just as numbers define an amount of something, so we must have
a way of defining nothing. Zero, therefore represents nothing or no-existence.
It is just as much a number as 6 or 7 is. For example:
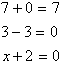
As we shall study, zero is an
important number as it helps in solving equations and defining infinity.
Negative numbers, in the simplest sense, are used to define those numbers that are the
result of a larger number being subtracted from a smaller one. Imagine a man
who has six pens. A young man comes to buy eight pens. How many are
left? The answer is not 0 but -2. The shopkeeper sells all six, but he still
needs two to give to the man. Negative numbers can therefore be thought of as
numbers that do not exist but should exist. They become positive when they take
on a physical existence otherwise they are missing pieces in a puzzle.
Our discussion of numbers has been limited to objects. This need not
be the case. Numbers can be used to represent abstract existences such
as 2 days, 3 years, 4 classes, etc. Recall how we defined the number to
be meaningless without referring to something. Three books meant one
book + one book + one book. The number can also be thought of as a
repetition of an occurrence. A day is defined as the rising of the sun,
setting, then rising again. This “ action” is cyclical and continues
indefinitely . We can therefore refer to each cycle of the sun rising as
one day and four days would then represent four cycles of the sun
rising.
Here we have extended the definition of the number to not only include objects but
also actions. The difference between an action and an object is a difficult one
to explain. While an object represents something we can see, touch, hold and feel,
an action is only that which happens. Actions refer to change or movement.
Therefore, an action's existence is defined by what takes place during that time
frame of a beginning and an end.
Numbers are not limited to objects and actions alone, they can also be used to count
ideas and other abstract concepts that exist only in the mind. Simply by
existing in the mind means it can be counted. When somebody says I have two
things to say to you, each thing is made up of a different choice of words,
phrases, not to mention the action or object it may refer to.
To conclude our discussion of the number here is a short definition.
Number - A symbol used to express an object's, action's or abstraction's
repetitive
nature.
Next section ->
Section 2.2 - Interpreting Numbers
