CHAPTER 11
Chapter 11 - Understanding Integration
Section 11.1 - Understanding Integration
In the previous chapter we took a highly theoretical
look at understanding the close relationship between the integral and its
derivative. The process of integration is an infinite summation of the
product
of a function of x,
f(x)
, and an infinitely small
Δx.
This infinite sum from x = a to
x = b is the total change in the
anti-derivative or integral of its function. The important point to
understand
was that a small change in a function df
is given by its derivative multiplied by an infinitesimal dx.
The goal of this chapter is to understand how to apply integration
whenever a variable is changing or a function is undergoing some change
over an interval. Consider a mathematical
function of the form.
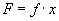
Assuming f and x represent
two
different conditions, then the situation F
is dependent on their product. In other words f and x are two
constants
whose product defines the dependent dimension, F.
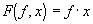
F
is therefore, a function of two independent conditions, f and x. If we let
x be a variable and f be a constant; we have:
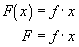
As x changes, F also
changes, since its value is only dependent on x and the constant f. Thus:
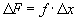
This should be rather obvious to
you. Now what if the condition, f, is
also a function of x? In other
words,
the value of f changes as x changes and is therefore, not a constant over an interval
from x = a to x = b. This modifies the relationship to:
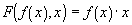
Since F is a function of f
and x and f is a function of x, then F is also some function of x
only, such that;
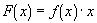
As the condition, f, is a function of x, then its value changes as x
goes from a to b. Therefore
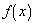can be assumed to be constant only over some infinitely small interval, dx. A small change in
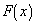df,
is proportional to the value of
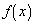multiplied by the
infinitely small change in x, dx.
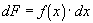
Dividing both sides by dx:
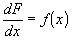
This extremely important result
defines the instantaneous rate change of
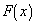with respect to x to be equal to
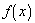. The relationship of
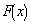to
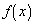is the same as
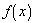is to
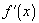i.e. a function and
its derivative. The only difference is the change in notation from
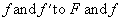. Multiplying both sides by dx again:
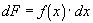
Integrating both
sides results in:
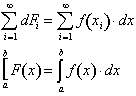
The result is still a bit abstract
and may not seem to be anything new to you. The important point to
understand
is that F is a function of two
independent conditions, f and x. If f is also a function of x,
then as x changes, f also changes such that its value
is
not constant over an interval from x
= a to x = b. Therefore an instantaneous
change in F, df, needs to be
defined
over an infinitely small interval over which f(x) is assumed to be constant.
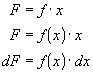
Integrating
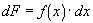from some value x = a to x = b gives us the net change in
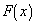over the interval.
Remember that
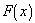is defined as the
anti-derivative of
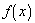
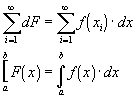
The result is the fundamental theory
behind integral Calculus. Take some time to think deeply and abstractly
about
what is going on in this derivation. Mathematically it represents the same
theory
derived in the previous chapter, but conceptually it explains integration
in a
new way. It allows us to analyze a changing situation in terms of
infinitesimal
changes which we can sum up to find the net change in the system as one
variable changes.
