Chapter 16 - Applications of the Exponential Function

" The most powerful force in the universe is compound interest." Albert Einstein

In this chapter we will take a look at just a few of the many interesting situations where the exponential function arises, i.e population growth and compound interest. The emphasis on the exponential function was that its base was multiplication, or it can be thought of as a repetitive multiplication function. We proved its derivative, but now we need to explain how to integrate it.

You may recall from Part I, that in integrating a function over any interval, we just added a constant to our integral. The derivative of the function with or without an added constant was still the same. The important point to realize here is that if we were calculating the integral over a definite interval from a to  b, then the constants are useless and take no part in the calculation. For example if the integral of f(x) is F(x) + C, then the integral from a to b is:

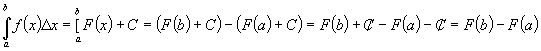
This tells us that the change in a function over an interval is independent of the constants that are added on. The constant are there to define the initial condition, such that for any, x, F(x) is simply plus or minus a constant. This will become clearer later on as we look at examples.

If constants are added on to polynomial functions, then they are multiplied on to exponential functions. What do we mean by this? When we are integrating the Logarithmic and exponential functions we can multiply constants that have no effect on the derivative, they are there only to satisfy initial condition. For example, the integral of 1/x is:

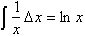
What is then the derivative of ln of a constant times x?

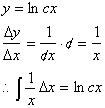
Note that we have not attached any limits to the integral, this is called the indefinite integral as it simply refers to any x over any interval. Suppose we were to integrate over a definite interval from a to b, then just as the constants in the polynomial functions canceled out, so will the constant in ln cx:

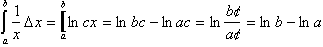
Therefore the constant plays no role in the change of function over an interval and is only there to define the initial condition..

Now let us move on to some applications, first a look at populations. Population growth is generally expressed as a percentage of the population per year. Such that a 3% growth rate means a population of  1000 people will see 30 new babies for the first year, 3% of 1030 for the next year and so on. No matter how large the population, there will always be 3% of the population wanting to have babies every year. We can express this relationship as follows:

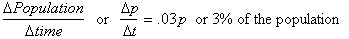
This can be written more generally as:

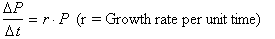
The only function whose rate of change or derivative is proportional to itself is the exponential function or:

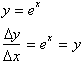
A more accurate way of solving this, is separating the variables and integrating the change in population from some initial to some final population, and integrating time from 0 to t.

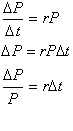
We can now integrate both sides over the limits just defined:

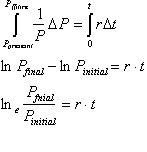
From the definition of the Logarithm we get:

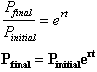
Note how the initial condition of a given population at t=0 is multiplied on to the exponential function and not added on, such that at t=0 we have:

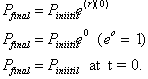
Consider the population of Pakistan, 120,000,000 people. If the birth rate is 3% per year, then what will be the population in 10 years?

We do not take the death rate into consideration is because the birth rate, takes into account both the birth and death rate such that it reflects the net or true growth in population per year. Our equation becomes:

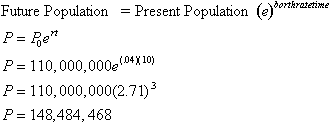
The population will therefore be over 148,484,468 people which represents an increase of 38,484,468 people in ten years. Note that this answer was not found by taking 3% of 110 million and multiplying by ten. This fails to work since it assumes that every year the population is 110 million, but this is clearly not the case, since the population is constantly growing and growing and 3% of the population is a larger and larger number. That is why 38,484,468 > 33,000,000.

If you are a skeptical person, like me, you will probably doubt how accurate our answer is. One argument might be that since the population is increasing every second and not only once a year, then 38,484,468 is not the exact increase as it is based on a yearly increase in population growth. In fact our answer does indeed take into consideration that babies are born every second and not only one a year. To understand this, go back to our proof of the derivative of the exponential function:

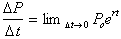
We are taking the limit as time goes to zero and similarly the integral:

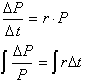
Is also based on ∆t going to zero. Furthermore the growth rate is a constant value and will always be 3%, in this case, regardless of how much time has passed in years, months or seconds. The fact remains that there will always be 3% of the population desiring to have babies.

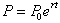is based on time going to zero, how can we be sure that when we solve for t =10, it is referring to ten years and not ten months or ten seconds later.

The way we are sure that 10 refers to years and not anything else, is by remembering that 3% growth rate is a per year figure. So.

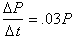
means that even though the growth rate is always 3%, it doesn't take into consideration that it takes around a year for a baby to be born, so that 3% per year means that the there will be .03P new babies per year, not per month.

Another fault with our equation is that it assumes that the 3 percent of the entire population at any given time t, has an equal desire to have a baby in one year. This is obviously untrue. Therefore our population equation is clearly flawed but the general idea is correct.

The continent of South Asia has an average growth rate of 2.5% per year. If the current population is 1.1 billion, in how many years will the population double or be 2.2 billion. Our equation:

Taking the natural log of both sides gives us:

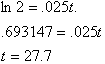
In 27 years the Population of South Asia will double.

In this next example we will take a closer look at the exponential function's role as a solution to the equation: 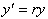. Hopefully all doubts will be cleared up now.

When one deposits money in a savings account, it is generally for letting the money earn interest. Interest is just money paid for the use of money. Interest rates are quoted as per year or 6% per year or 9% per annum( per year). So a 6% rate would mean that $1000 would earn 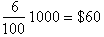. This is called simple interest since the money only earn interest once a year.

Compound interest on the other hand, is where the interest earns interest. So $10,000 put into an account that earns 6% interest, compounded quarterly or every three months, undergoes a series of calculation. In each quarter we add the interest earned from the previous quarter to the amount of money in the bank to get our new balance for the next quarter. Therefore the interest earned in the previous quarters adds to the interest earned in the following quarters

Quarter 1:

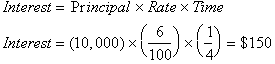
Quarter 2:

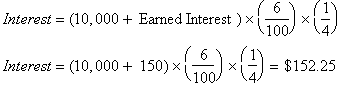
Quarter 3:

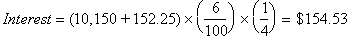
End of 1 Year:

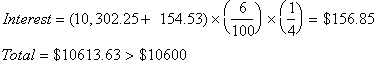
The difference is not much since the amount of interest earning interest is small. The balance in the bank after one period for money compounded n times a year can be found by:

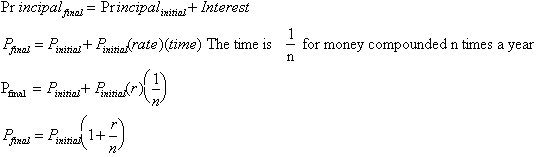
This last formula gives us the new balance after the first time it was compounded. To find the amount for the second compounding period we multiply by:

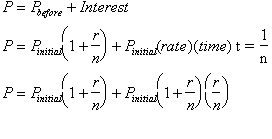
Factoring out a 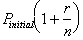gives us:

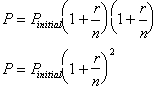
The money in the bank after the 3.rd and 4.th it has been compounded is given by 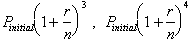. By observing the pattern we can conclude that the balance at the end of the year, when the money has been compounded n times is:

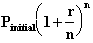
If $10,000 were put into a savings account that gives an interest rate of 6%. compounded quarterly,

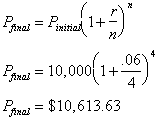
If this new balance were put into the same account for another year we would have:

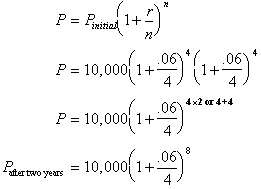
The formula then for calculating the new balance, or how much money is in the bank after t years compounded n times is:

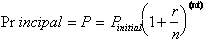
The exponent (nt) refers to how many times the money has been compounded. If in one year it is compounded n times, then in t years it is compounded nt times over the t years.

If the same money were compounded infinite times this would mean that the interest is constantly earning interest. The interest earned over a small change in time is added to the previous balance, creating a new balance on which the interest earned over the next small time interval is based on. Therefore the rate at which the money is changing is proportional to the amount of money in the bank times the interest rate.

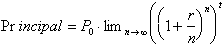
Let us examine this familiar looking limit in the brackets, 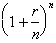. It looks similar to the definition for e, except for the r, interest rate which is constant throughout the time interval. To evaluate this recall that the limit as Δx goes to zero of x/Δx and Δx/x were infinity and zero, respectively. This is true regardless of the value of x, since its value was fixed and did not change. Therefore by raising 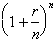to the 1/r power gives us:

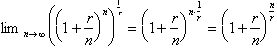
Now as n tends to infinity, r/n goes to zero, and n/r goes to infinity. This gives us the familiar answer, e.

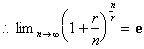
Raising both sides to the, r, power we get:

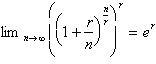
This gives us the limit of what we were initially looking for:

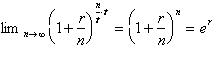
Or more generally for any x,

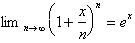
Returning back to our initial problem of calculating the Principal in an account that compounds interest infinite times per year:

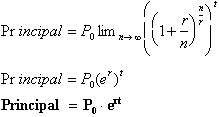
This important answer could also have been arrived at by realizing that money that is put into an account that compounds interest infinitely is changing at a rate proportional to the amount of money in the bank, times the interest rate. For example if at t=4, the amount of money in the bank was $10000, and the interest rate was 6%, then at that instant the money would be changing at the rate of $600 a year. As the money changes then so does the amount of money in the bank, such that  our equation becomes:

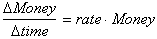
We can call Money, Principal or just P, and separate variables:

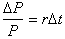
We can integrate this equation to solve for P in terms of r and t. We integrate time from 0 to t, and Principal, from P at t=0, to some final value of P.

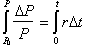
This yields the solution:

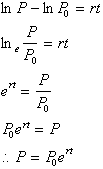
This last answer is the same answer we derived using the definition of compound interest, which gives us the amount of money in a bank after t years and infinite compounding with an initial deposit of P₀. Differentiating this equation with respect to time:

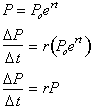
Despite how difficult it may seem to explain this change the fact remains that the money is changing at a rate proportional to the amount of money itself, such that as the money begins to change over a small change in time, the amount of money in the bank changes by a small amount creating a new balance that is only accurate for the next Δt . It is really this simple.

In this example we will compare simple interest to compound interest. Consider a poor college student who decides to put his summer earnings of $2000 into a savings account for 3 years. His choices are to City Bank that offers a simply interest rate of 3.2% per year or Carolina Bank that offer an interest rate of 2.9% compounded continuously. Where should he put his money? Also note that City Bank offers a free T-shirt for opening a savings account.

Lets first consider City Bank. The rate at which his money will be changing is the rate of interest time the amount of money in the bank or (3.2/100)(2000) = $64/year. Remember this is the definition of simple interest, the rate at which your money is changing is only dependent on how much Money you initially open the savings account with.

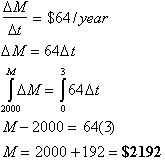
With Carolina Bank, the interest rate is 2.9% compounded continuously. We can just go directly to our equation for continuous compounding:

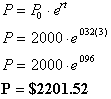
This tells us that the interest earning interest only contributed to an extra $9.52, barely more than the cost of the shirt. This is because the interest earned was small, and the interest it earns is even smaller. Now if we were to put the money on for 30 years, then the interest earned will have enough time to earn some substantial interest.

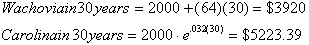
In simple interest the amount of money in the bank remains constant, while in compound interest the balance is increasing constantly.

Just as exponential functions increase with rates proportional to the function itself, they can also decrease. This happens when:

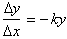
Whose solution is simply:

The evolution of living beings is also based on the priniciples of exponential growth. Most people can not understand how small changes to populations per generation can lead to large differences in species over long periods of time. This works exactly the same way money grows to a large amount when interest is compounding.

Sean B. Carroll writes in his book, The Making of the Fittest:

In the case of evolution, the amount of the initial investment is analagous to the number of individuals in a population with a trait. And the interest rate is analogous to the small selected advantage that trait confers on those individuals that carry it.

While the time required for one trait to become prevalant in a population is greater than one lifetime, it is often no more than a few hundred generations. This is a blink of an eye in geologic time. This tells us that small differences among individuals when compounded by natural selection over time really do add up to the large differences we see among species.

This concludes our study of the exponential and logarithmic function. It is important to understand the differences and similarities to the polynomial function. The base of the exponential function is multiplication and exponential growth can be thought of as repetitive multiplication. In this chapter we saw how this applies to multiplying populations and multiplying money.

Questions

1. The power of compound interest lets you amass large wealth as long as you start investing early. In the early years your investment will grow linearly , but after some years you will see the investment grow very fast. Make a bar graph in excel for investing $10,000 once a year for 30 years. If you do not have excel, you can download either Open Office or Gnumeric , both are free spreadsheet softwares. Assume the interest is compounded continuously at a rate of 6%.

   Write a formula to calculate the value of the $10,000 at the end of the first year. Then in the next row add $10,000 to the new principal and use the same formula to find the value of the new principal afer that year ends. The graph you make should illustrate the power of investing early in life and reaping large rewards towards the end .

2. Exponential decay occurs whenever the rate at which the function is decreasing is proportional to the function itself. Consider the element Uranium that undergoes radioactive decay at the rate of 12% of the material per year. This decay rate, 12%, is independent of the amount of material present. Find the time taken for half of Uranium to disappear, or the half life.

   

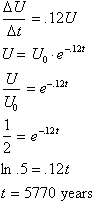
   This half life is true for any amount of material. A 1000 kg sample and a 1 kg sample will both take the same time to reduce to half their original mass.