Chapter 8 - Understanding the Derivative
Chapter 8 - Understanding the Derivative
Section 8.1 - Using the First Derivative
In this chapter we will take a close
look at the definition of the derivative and its relation to its
anti-derivative. We will see how the graph of the anti-derivative can be
accurately described by just looking at the derivative function only.
From the definition of the derivative,
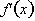is the derivative of
a function
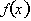. The derivative of a function tells us how fast f is
changing relative to the independent variable, x. Thus the derivative refers
specifically the rate of change of the anti-derivative function with respect to
x. Rate of change is also synonymous with the slope of the tangent line to the
graph at a particular point.
Therefore, a function and its derivative are closely related and
knowing just the derivative can tell us a great deal about the behavior of its
anti-derivative. Since the derivative of a function is derived from the
definition of a derivative as:
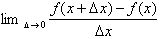, we can work with the definition to find the anti-derivative
when only the derivative is known. Also recall how differentiation is based on
a limiting or subtracting process and dividing; therefore working backwards
would tell us that we should be adding and multiplying.
We will develop on this later, however, let us first look at how
we can use f’(x) to obtain equilibrium points on the graph of the
anti-derivative or f(x).
Equilibrium points are by
definition, points on the graph refer to static situations
where the rate of change is zero. Thus a change in the independent variable
results in no change in the dependent variable. Equilibrium sate generally
occurs when a situation has reached a critical maximum value and then decreases
or where a situation has reached a critical minimum value then increases.
Equilibrium and critical values of a
function can refer to different things depending on the phenomena being
studied. Therefore we will restrict ourselves to the geometric interpretation
of an equilibrium as a point on the graph where the rate of change is zero.
Since the rate of change is zero, the tangent to the graph at this point will
be a horizontal line.
A horizontal tangent tells us that
the derivative’s value at the equilibrium point is zero. Such situations occur
when the graph has reached a maximum or minimum value.
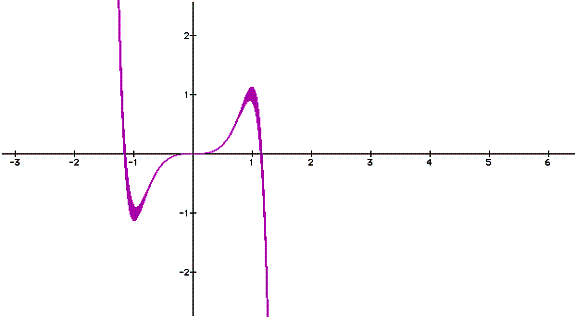
Horizontal tangent may also exist,
but not necessarily, when the concavity of a graph changes.
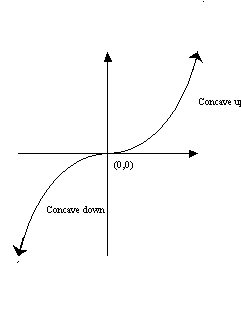
A change in concavity occurs at
points on the graph called inflection
points. As we shall soon study, the derivatives value at an inflection does not
have to be zero. Therefore we will restrict our definition of equilibrium
points to reflect either maximum or minimum values on the graph.
For example to find equilibrium
points for the function,
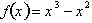. we first need to differentiate it to get,
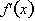. The derivative,
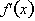, tells us the instantaneous rate of
change of function,
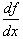, at any point x. Since we want to find points where the rate
of change of f(x) is zero, we need to
set
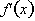equal to zero to find those values of x which the satisfy the equation,
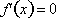. Doing this for
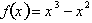results in:
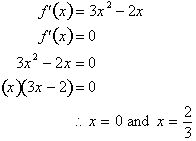
This tells us that at both x=0 and
x=2/3 there exists an equilibrium point, which is confirmed by the graph of the
function,
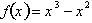
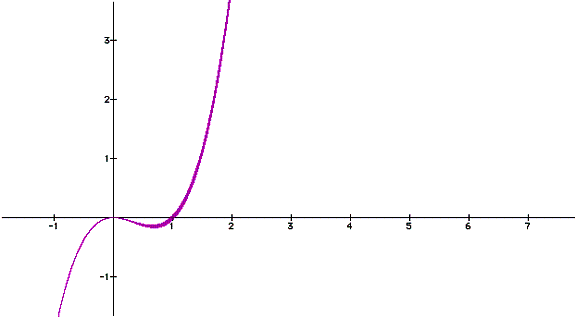
Having
found the critical points, how do we classify them as either maximums or
minimums? Obviously this can be done by just looking at the graph of
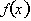, but the purpose of this chapter is to understand how to only use the
derivative,
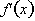to approximate the
behavior of the function
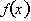. To determine whether our equilibrium points are either
maximum or minimums we need to evaluate points left and right of the
equilibrium points to determine where the function,
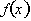, is increasing or decreasing.
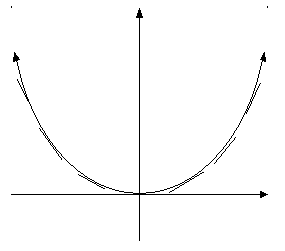
A minimum is defined as the bottom of a U-shaped or concave up graph.
If the graph is concave up then the slope or rate of change is positive to the
right of an equilibrium point and the function is increasing to the right of
that point. To the left of the equilibrium point, the slope is negative which means the function is decreasing till
it reaches the equilibrium point. To better understand this, look at the
following graph of a concave up portion of a graph. Notice how the function
decreases till it reaches the equilibrium point then rises after passing it.
Similarly if the rate of change of
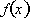were negative on the
right side and positive on the left side of the equilibrium point, then we get
an inverted U shaped or concave down graph. A concave down graph thus reflects
a maximum value at the equilibrium point.
If the slope is both positive or
negative on either side of the equilibrium point then we get an inflection
point that represents where the concavity changes from a U
shape to an upside down U
shape or vice-versa. The following graph summarizes the above conclusions.
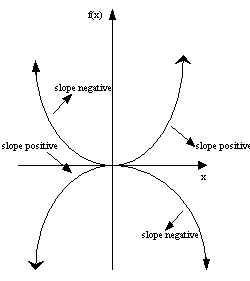
Next section ->
Section 8.2 - Using the Second Derivative
