Chapter 8 - Understanding the Derivative
Chapter 8 - Understanding the Derivative
Section 8.2 - Using the Second Derivative
The first derivative allows us to
define equilibrium points on the graph of a function,
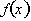. By evaluating points to the left and right of the
equilibrium point we can classify these points as either maximums or minimums
and thus determine the concavity of the graph. Without having found the equilibrium points it is extremely
difficult to determine the behavior of a function over an interval. The sign of
the first derivative only tells us if a function is increasing or decreasing;
however, a function can increase or decrease in two way. For example consider
the graphs of the following two different functions.
In both cases the function is
increasing and the first derivative is always positive; however each function
increases in a different way i.e. one increases concave up and the other
increases concave down. Using the first derivative only, we would have to know
not only where its positive or negative but also how the first derivative is
changing i.e. positive and increasing, negative and increasing etc.
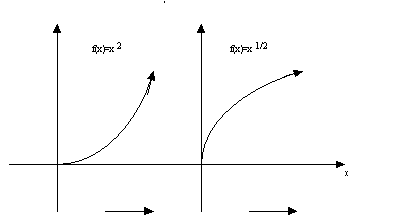
For the first graph
is positive and increasing thus the graph of f(x) is increasing and concave up. For the
second
graph,
is also positive but
is decreasing. Thus the graph of
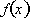
is concave down. The process of looking only at the graph of
the first derivative to understand how
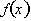behaves is an
extremely abstract and difficult one. To quicken and simplify our work we can
use the function’s second derivative
to conclude where the graph is concave up or down. This information along with
the fact that the derivative is either positive or negative over an interval
will be enough to accurately determine a function’s behavior.
Recall that a property of a concave
up part of a graph is that its slope or rate of change is always increasing.
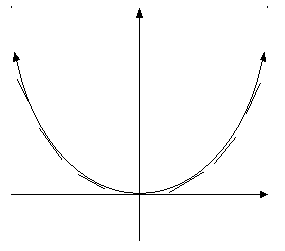
On the left side the slope is
negative; however, as x increases the slope gets less and less, -5, -3, -2,
till it reaches 0, from where on it increases to 1, 5, 6, etc. We can then
conclude that the rate at which the slope is changing must be positive or the
graph of the derivative is increasing. Since the derivative’s value is constantly
increasing, then the rate of change of the derivative, given by
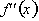will be positive.
Remember that positive rate of change implies that the function is increasing
over that interval, while a negative rate of change implies the function
decreases as x increases.
In a concave up graph the derivative
is increasing, such that the second derivative over this interval will be
positive. Working in reverse we arrive at an important conclusion. If the
second derivative is positive over an interval, then the first derivative is
increasing, implying that the graph of the original function,
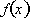is concave up. This is true because the rate of change of a
concave up graph is always increasing.
The reverse is true for concave down
graphs. If the second derivative is negative then the first derivative is
decreasing, implying that the original functions graph is concave down over the
interval. The following graph summarizes the conclusions:
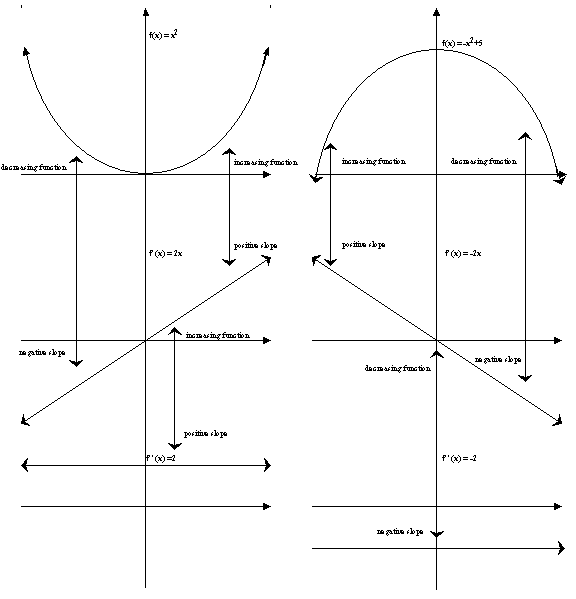
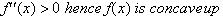
Though all the information
concerning the behavior of f(x) can be obtained from studying its derivative,
we can quicken and confirm our sketches by looking at the functions second
derivative. Without having found any equilibrium points we can accurately
determine the behavior of
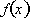over an interval by
using the signs of both the function’s first and second derivative
simultaneously. Four possibilities may exist for the signs of the derivatives.
Both
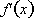and
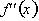are positive over an interval. Therefore
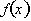is increasing and concave up.
2.
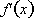is positive but
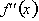is negative. Thus
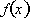is increasing and concave down
3.
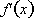and
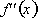are negative, in which case
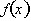is decreasing and concave down.
4.
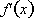is negative but
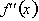is positive, thus
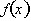is decreasing and concave up.
Next section ->
Section 8.3 - The Systematic Use of the Derivatives
