CHAPTER 7 - Study of Free Falling Bodies
Chapter 7 - Study of Free Falling Bodies
Section 7.3 - Initial Conditions of Motion
The concepts of
forces, accelerations, velocities and distance are not limited to free-fall
motion. Constant accelerations exist in many other physical phenomena’s. Before
ending we need to understand how we can modify our equations of motion to be
consistent with any initial conditions that may exist. For example, a ball may
be dropped with an initial velocity or a car may accelerate from a certain
distance from a starting point.
If an object was moving at constant velocity,
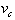, its velocity function would be:
From the definition of the derivative, the derivative of a constant function of
the form
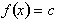is zero because:
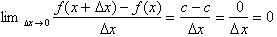
Therefore the derivative of
the velocity function is:
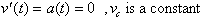
Looking back at our free-falling body, we know that its
acceleration was
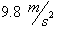. This can now be written as:
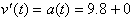
The anti-derivative of this
acceleration function is then:
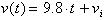
Remember that the
anti-derivative of zero is a constant. At t=0
we have the initial condition:
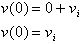
We call
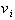
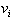, or the velocity of the object at t= 0. It represents a
situation that may exist when the initial condition is zero. When
anti-differentiating we need to remember to add a constant along to reflect the
initial conditions that may exist in the situation. For example if a car is
traveling down the highway at 82 mph , suddenly sees a cop, and then steps on
the pedal, accelerating the cart at 3 mph/s, then its velocity at any time t,
were t is measured as soon as he steps on the gas is:
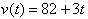
We know that the velocity function of a free-falling body
is:
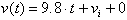
The anti-derivative of this
function gives us the distance covered as a function of time:
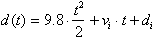
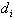is the objects
initial position at t=0. Our result
can be generalized for initial acceleration
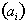
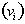or distance as follows:
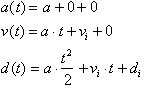
Questions
Consider the following three cases for a free-falling
body:
1 - A ball is dropped from rest from the top of a building.
2 - A similar ball is dropped from the same spot with an
initial velocity of 10 m/s
Find the distance function
(distance covered as a function of
time) for each case.
-
Consider three cars that pass a certain starting point.
Car 1 - starts from rest with a constant acceleration of 6
m/s/s
Car 2 - Has an initial velocity of 50 km/hr and maintains
this constant velocity with no
acceleration.
Car 3 - Has an initial velocity of 20 km/hr and an
acceleration of 4 km/hr/ sec
Car 4 - starts 5 km in front of all the other cars with no initial
velocity but an acceleration of 7 km/hr/sec.
Derive the distance
function for each car with reference to the distance covered from the
staring point.
Graph the distance function for each car.
-
Last, determine at which distance each car will pass
each other. You can do this by either looking at where the graphs of the paths
intersect or by setting the distance functions equal to each other and solving
for time.
Solutions
- d(t) = 4.9t^2
-
d(t) = 4.9t^2 + 10t
-
car1: d(t)=10.8t^2
- car2: d(t)=50t
- car3: d(t)=2t^2 + 20t
- car4: d(t)=3.5t^2 + 5
- car1 and car2 intersect at about 235 m at a time of about 4.8 seconds
- car1 and car3 intersect at about 55 m at a time of about 2.4 seconds
- car1 and car4 intersect at about 10 m at a time of about 1 second
- car3 and car4 intersect at about 6 m at a time of about .5 seconds
- car2 and car3 seem to never intersect, unless the intersection is at time
much greater than 6 seconds
Next section ->
Section 8.1 - Using the First Derivative
