CHAPTER 7 - Study of Free Falling Bodies
Chapter 7 - Study of Free Falling Bodies
Section 7.2 -
Understanding Free Fall Motion
Having laid down
the conceptual basis of what velocity, acceleration and forces are, we can now
study the motion of free falling bodies on earth. An object falls to earth
because of the gravitational force of attraction that the earth experiences for
the object. What then is gravity? From Newton’s law of gravitation, the force
attracting two bodies is given by:
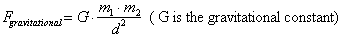
To derive this, think of a unit mass of 1 kg separated a
distance from a larger mass, M. The
gravitational force is the force of attraction the larger mass expresses for
the unit mass and vice-versa. Observation confirms that the gravitational force
is proportional to mass the larger body and decreases with the square of the
distance separating them. The reason it is distance squared and not just
directly related to the distance is because masses are 3-dimensional. In
3-dimensional space, properties are related to the projected areas as opposed
to 2-dimensional geometry that are dependent on the length only. Therefore, the
gravitational force between the two masses is:
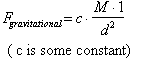
If the unit mass was replaced by a mass m, the force of attraction would be m times the amount it was with the unit
mass.
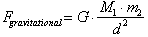
G replaces “c” as a gravitational constant
determined from experiments. The gravitational force of earth acting on a body
of mass
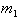located
near the surface of the earth is
then:
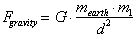
Since most of our free falling bodies occur near the
surface of the earth, we can take d,
to be the radius of the earth. Substituting the known values in along with the
value for G, reduces the equation to:
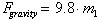
Since force equal ma, we have:
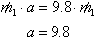
This important result tells us that the acceleration of a
body of any mass is 9.8 meters per
second per second near the surface of the earth. The gravitational force acting
on a body near the surface of the earth would be its mass, m, times the constant acceleration, 9.8. For those who have a
ground to hold them up this does not mean much but for a free-falling body in
air its acceleration as it falls toward the earth will be a constant
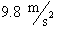, regardless of its mass. A body of twice the mass will be
pulled in by twice the force, but the acceleration due to the force of gravity remains the same.
This may sound a bit confusing but just remember any body
will fall to the earth with a constant acceleration, independent of its mass. In terms of particle motion, mass means nothing for a falling body! While
the gravitational force increases with mass, the acceleration remains the same.
We can now write the acceleration function for a falling
body near the earth’s surface as:
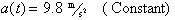
Since acceleration as a function of time is by definition
the derivative of the velocity function with respect to time then what we have
is the same as:
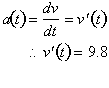
The derivative of the velocity function (acceleration) is
9.8. Since we know that the derivative of any function
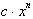is
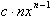then we can easily
find the velocity function since we know what its derivative is.
The process of finding a function, given its derivative
is known as anti-differentiation. In
this case 9.8 can also be written as
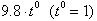. We see that:
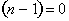
Therefore n equals 1. Consequently the anti-derivative of
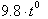is
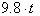. This should hopefully be obvious since the derivative of
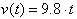is just
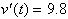. We now know that velocity as a function of time is:
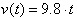
whose derivative with
respect to time is:
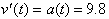
The graph of the velocity function is a linearly increasing function with constant rate of
change or slope
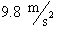
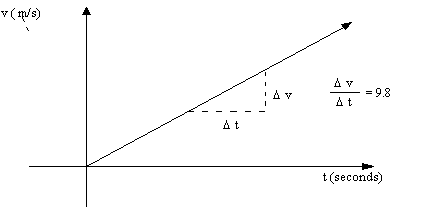
This graph of the velocity function gives us the objects
velocity as any time t, assuming that air-resistance is negligible. For example
at t= 10 seconds, the object’s velocity is:
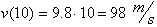
At t= 94 seconds its
velocity is:
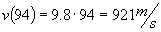
Or almost 30,000 km/ hr. Due to air-resistance no object
reaches such high velocities. Remember the greater the height it is dropped
from the more time it has to increase its velocity or accelerate before it
slams into the earth.
Now how do we find the distance function or the distance
covered from the point of dropping the object. From the definition of velocity
we know that:
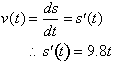
Since
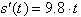, we
have n=1 so its anti-derivative will be
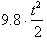where the derivative
of
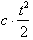is
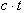ct = 9.8t.
The solution is then:
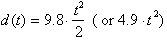
The derivative of this
function is the velocity function or:
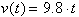
We can graph the distance function
.
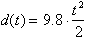The graph gives us the vertical distance traveled from where it was dropped at
any time t.
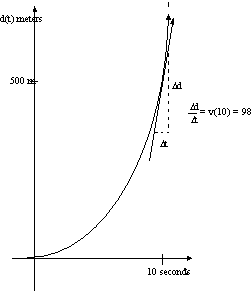
Clearly as time, t, increases, the rate at which distance is
being covered is very great . For example between t= 0 s to t =5s, the object has covered totally.
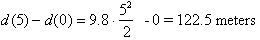
Or the object has covered 112.5 meters in the first five
seconds of its free-fall. However from t = 20 s to t = 25 s, the object has
covered:
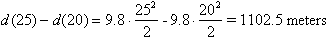
The object has covered more than a kilometer during this
five second interval!! This should make sense because initially the body’s
velocity is small and thus does not cover much distance over a time interval
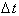;. However, after some time its velocity has increased ( look at the graph of the velocity
function
graph), such that over a same interval
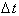, the object covers a greater distance. Remember constant
acceleration means that the velocity is increasing linearly with time and
distance increases with the half square of time.
Next section ->
Section 7.3 - Initial Conditions for Motion
