CHAPTER 5
Chapter 5 - Differentiating Functions
Section 5.3 - Differentiating Products
of Functions
Consider the following function:
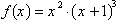
If we let
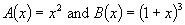, then f(x) can be expressed as the product of the two function A(x)
and B(x) such that:
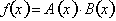
We can differentiate products of
functions by using the definition of the derivative. A small change in f can be written as:
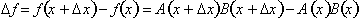
Next, divide by
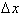to calculate the rate
of change of f with respect to x:
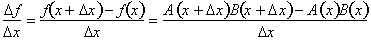
Taking the limit as
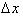goes to zero gives us
the instantaneous rate of change of f
with respect to x, or the derivative
of f(x).
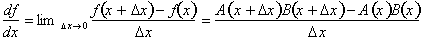
From the definition of the derivative we know that:
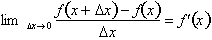
Multiplying both sides by this
infinitely small
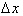
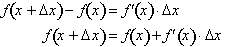
Since both A(x) and B(x) are
functions of x, then
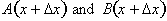can be substituted with
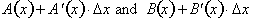respectively. Note that this substitution only holds true for
going to zero. We now have:
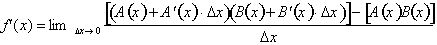
Expanding the numerator:
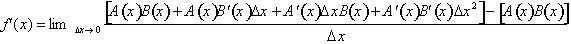
Canceling terms
and dividing through by
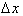reduces it to:
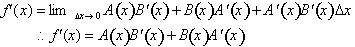
Thus the derivative of a function f(x) that is a product of two functions
of x, is simply the product of the
first function and the derivative of the second function plus the product of the second function and the derivative of the
first function.
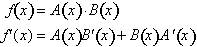
Next section ->
Section 5.4 - Differentiating Functions of any Power of N
