CHAPTER 11
Chapter 11 - Understanding Integration
Section 11.4 - Engineering Applications
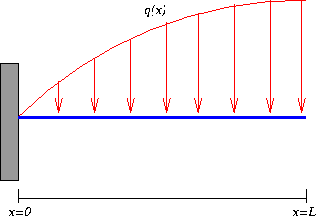
Cantilever Beam
A structural beam in Civil Engineering is designed to support load over
a span. A specific type of beam is a cantilever beam which is beam with
one end completely fixed so that it can not move. A picture is shown below:
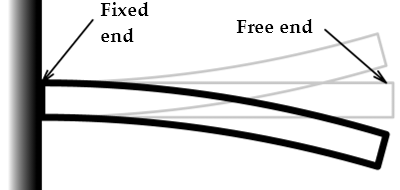

If a load/force is applied at the end of the beam, the beam will
bend downwards. Try this with a ruler in your hand to see how it bends.
When a load is applied at the end the beam will experience the highest
stress at the end where it is fixed. The stresses it experiences are
proportional to how high the load is and how far the load is from the
fixed end. In engineering, the term 'Bending Moment' is calculated from
the product of the load multiplied by the distance . The greater the bending
moment , the greater the chance it will break . Therefore:
Bending Moment = Load X Distance
In the example below of a single load at the end of the beam , the bending moment
at the fixed end would be Load times the distance, d.
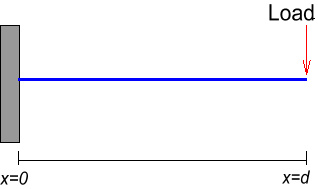
How would we find the bending moment for the case shown below?
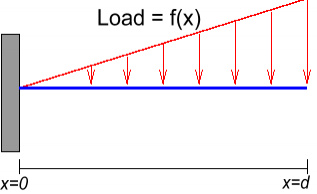
Here a distributed load is
increasing along the span of the beam with a triangular
distribution. Triangular distributed loads are
found commonly when a liquid is exerting pressure on a wall with the pressure
increasing
with the depth . An example would be the walls of your swimming pool. As
the water goes deeper, they exert a linearly increasing pressure on the walls of the
pool.
Since our distributed load is changing with the span of the beam, we need to apply our
systematic approach to integration to solve the problem.
Step 1 - Determine the form of the functional relationship between
the interacting conditions. This is synonymous with writing the
equation, where every dimension is assumed to be a constant:
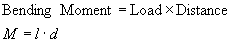
In Civil Engineering, a distributed load is expressed as a constant in units of load
per unit distance. For
the case where the loading is a uniform rectangular distributed
load over the span as shown below:
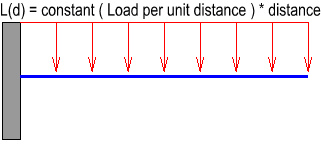
We can write:
Load = some constant * distance
The constant is in units of load/distance and its value depends
on the magnitude of the distributed load. Therefore the constant multiplied
by distance equals the total load acting over that distance.
Step 2 - Identify which dimension is changing with respect to another
dimension and determine the independent variable.
In our triangular distributed loading case
the constant changes linearly with distance or:

Step 3 - Write the differential dF, as a product of f(x) and an infinitely small change in the independent variable x, dx.
Substituting back into our equation for bending moment:
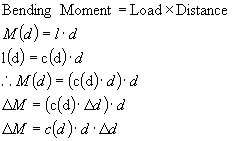
Step 4 -
Integrate both sides of the function from some value x=a to x=b
to calculate the net change in the dependent dimension F.
In the triangular loading case, c(d) just equals some constant, c multiplied by d.
We could certainly have parabolic and even exponential distributed loading functions. But for
triangular loading, we just need to replace c(d) with constant times d or:
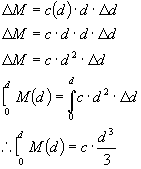
Questions
Determine the bending moment for this parabolic type of loading: