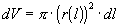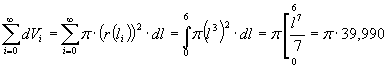CHAPTER 11
Chapter 11 - Understanding Integration
Section 11.2 - Geometric Applications
Let us consider some geometric
examples of integration that are easy to visualize and understand. Following
geometric applications we will move onto more physical applications from
science and engineering.
The first example we will study is
that for finding the area of a shape whose height is changing with its length. By
definition the area of a rectangle is given by the equation:
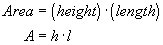
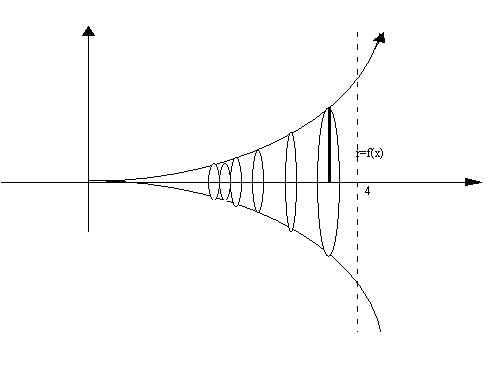
What if the height of a particular
shape were changing with respect to its length, expressed by the function,
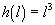? The graph of the function and shape would look like this:
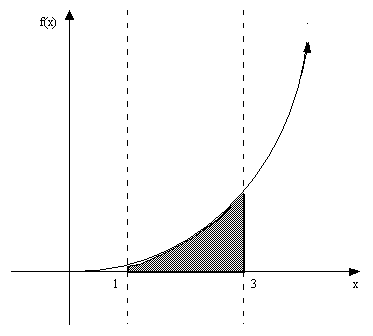
What is peculiar about the shaded
area? The only apparent characteristic is that its height is changing with the length
such that as the length increases the height increases.
Therefore the area
of the object is not a simple matter of:
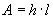
In the graph, height is a function
of length. The area equation for the shape now becomes:
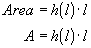
Over an infinitely small length, dl, the area of one rectangle has constant height,
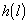and length, dl .
Over an infinitely small interval, the area under the curve changes by the
area of one rectangle. This can be expressed as:
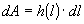
The infinite sum of the inscribed
rectangles over an interval of l=a to l=b corresponds exactly to the net
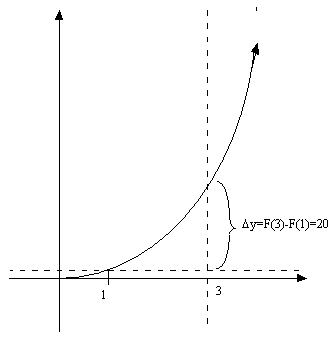
change in the area of the shape, or the area under the curve from l=a to l=b. Thus the area of the shape from l=1 to l=3 is:
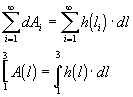
Evaluating the integral:
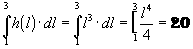
The total area
is then 20,or looking at the graph of
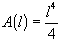
It is important to understand, that
the function
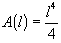gives us the net
change in the area defined by a changing height,
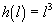as l changes from
some value a to b. Since
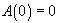then in this unique
case
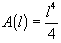will give us the area
the shape for any length, l. However keep in mind that we are calculating how
much a situation changes, as its
defining conditions change.
Now let us look at volumes. Let us
say we take the same shape with length, l,
and height,
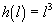and revolve it around
the x-axis. How do we find the volume of the conical cylinder generated?
All we have is a cylinder of varying
or changing radius. The radius is give as a function of length by;
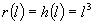
The equation for the volume of a cylinder is:
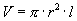
As the length goes from some value, a to b the radius changes with respect to the length. The equation can
only hold true over an infinitely small interval, dl. The change in the volume of one infinitely small cylinder with
length, dl, is
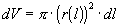
The net change in the volume of the
cylinder as the length changes from 0 to 6 is found by integrating the
differential,
